Jika A dan B adalah matriks yang mempunyai ordo sama, maka penjumlahan dari A + B adalah matriks hasil dari penjumlahan elemen A dan B yang seletak. Begitu pula dengan hasil selisihnya. Matriks yang mempunyai ordo berbeda tidak dapat dijumlahkan atau dikurangkan.
Jumlah dari k buah matriks A adalah suatu matriks yang berordo sama dengan A dan besar tiap elemennya adalah k kali elemen A yang seletak. Didefinisikan: Jika k sebarang skalar maka kA = A k adalah matriks yang diperoleh dari A dengan cara mengalikan setiap elemennya dengan k. Negatif dari A atau -A adalah matriks yang diperoleh dari A dengan cara mengalikan semua elemennya dengan -1. Untuk setiap A berlaku A + (-A) = 0. Hukum yang berlaku dalam penjumlahan dan pengurangan matriks :
- a.) A + B = B + A
- b.) A + ( B + C ) = ( A + B ) + C
- c.) k ( A + B ) = kA + kB = ( A + B ) k , k = skalar
Matriks Balikan (Invers)
JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan
 ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan
( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan  . Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.Matriks A =
 dapat di-invers apabila ad - bc ≠ 0
dapat di-invers apabila ad - bc ≠ 0Dengan Rumus =
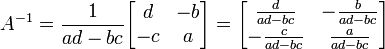
Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan

Contoh 1:
Matriks
-
- A =
 dan B =
dan B = 
- A =
-
- AB =

 =
=  = I (matriks identitas)
= I (matriks identitas)
- AB =
-
- BA =

 =
=  = I (matriks identitas)
= I (matriks identitas)
- BA =
 (B Merupakan invers dari A)
(B Merupakan invers dari A)Contoh 2:
Matriks
-
- A =
 dan B =
dan B = 
- A =
-
- AB =

 =
= 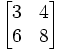
- AB =
-
- BA =

 =
= 
- BA =
Contoh 3:
Matriks
-
- A =

- A =
Jawab:

Contoh 4:
Matriks
-
- A =
 , B =
, B =  , AB =
, AB = 
- A =
-
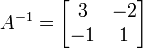 ,
, 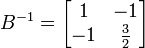 ,
, 
-

 =
= 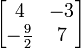

Transpose Matriks
Yang dimaksud dengan Transpose dari suatu matriks adalah mengubah komponen-komponen dalam matriks, dari yang baris menjadi kolom, dan yang kolom di ubah menjadi baris.
Contoh:
Matriks
-
- A =
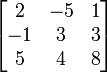 ditranspose menjadi AT =
ditranspose menjadi AT = 
- A =
Matriks
-
- B =
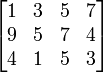 ditranspose menjadi BT =
ditranspose menjadi BT = 
- B =
Rumus-rumus operasi Transpose sebagai berikut:
-
- 1.

- 2.
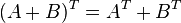 dan
dan 
- 3.
 dimana k adalah skalar
dimana k adalah skalar - 4.
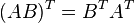
- 1.

Tidak ada komentar:
Posting Komentar