Matriks Diagonal
Sebuah matriks bujursangkar yang unsur-unsurnya berada di garis diagonal utama dari matriks bukan nol dan unsur lainnya adalah nol disebut dengan matriks diagonal. Contoh :
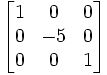

secara umum matriks n x n bisa ditulis sebagai

Matriks diagonal dapat dibalik dengan menggunakan rumus berikut :
 =
=

jika D adalah matriks diagonal dan k adalah angka yang positif maka
 =
=
Contoh :
A=

maka
 =
=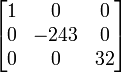
Matriks Segitiga
Matriks segitiga adalah matriks persegi yang di bawah atau di atas garis diagonal utama nol. Matriks segitiga bawah adalah matriks persegi yang di bawah garis diagonal utama nol. Matriks segitiga atas adalah matriks persegi yang di atas garis diagonal utama nol.Matriks segitiga

Matriks segitiga bawah

Teorema
- Transpos pada matriks segitiga bawah adalah matriks segitiga atas, dan transpose pada matriks segitiga atas adalah segitiga bawah.
- Produk pada matriks segitiga bawah adalah matriks segitiga bawah, dan produk pada matriks segitiga atas adalah matriks segitiga atas.
- Matriks segitiga bisa di-inverse jika hanya jika diagonalnya tidak ada yang nol.
- Inverse pada matriks segitiga bawah adalah matriks segitiga bawah, dan inverse pada matriks segitiga atas adalah matriks segitiga atas.
Matriks segitiga yang bisa di invers
A =

Inversnya adalah
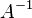 =
=
Matriks yang tidak bisa di invers
B =

Matriks Simetris
Matriks kotak A disebut simetris jika
Contoh matriks simetris

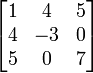
Teorema
- Jika A dan B adalah matriks simetris dengan ukuran yang sama, dan jika k adalah skalar maka
 adalah simetris A + B dan A - B adalah simetris kA adalah simetris
adalah simetris A + B dan A - B adalah simetris kA adalah simetris 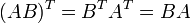
Jika A adalah matriks simetris yang bisa di inverse, maka
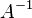 adalah matriks simetris.
adalah matriks simetris.Asumsikan bahwa A adalah matriks simetris dan bisa di inverse, bahwa
 maka :
maka :
Yang mana membuktikan bahwa
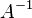 adalah simetris.
adalah simetris.Produk
 dan
dan 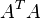
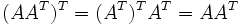 dan
dan 
Contoh
A adalah matriks 2 X 3
A =

lalu
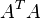 =
= 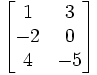
 =
= 
 =
= 
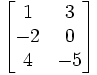 =
= 
Jika A adalah Matriks yang bisa di inverse, maka
 dan
dan 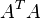 juga bisa di inverse
juga bisa di inverse

Tidak ada komentar:
Posting Komentar