Penyelesaian No 6

Tunjukan bahwa Z₄adalah merupakan suatu Ring.
Penyelesaian :

Tabel

Daftar Cayley (Z₄, +) dan (Z₄, .)-0

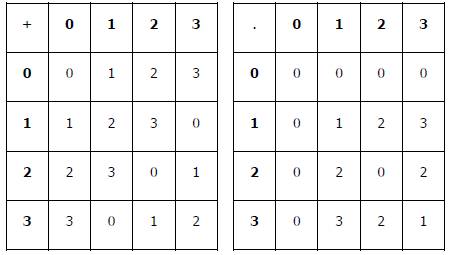
Dari tabel di atas akan ditunjukan bahwa Z₄ = {0, 1, 2, 3} merupakan suatu Ring bila memenuhi :
1. Grup Komutatif terhadap penjumlahan (Z₄,+)
-          Tertutup
Ambil sebarang nilai dari Z4, misalkan 0, 1, 2, 3 ∈ Z₄
1 + 0 = 1
1 + 1 = 2
1 + 2 = 3
1 + 3 = 0
karena hasilnya 0, 1, 2, 3 ∈  Z4, maka tertutup terhadap Z4
-          Assosiatif
Ambil sebarang nilai dari Z6, misalkan a = 2, b = 1 dan c = 3 ∈  Z4
(a + b) + c = (2 + 1) + 3 = 3 + 3 = 2
a + (b + c) = 2 + (1 + 4) = 2 + 4 = 2
Sehingga :
(a + b) + c = a + (b + c) = 2
maka Z4 assosiatif
-          Adanya unsur satuan atau identitas
Ambil sebarang nilai dari Z4

• misalkan 0 ∈  Z4
  0 + e = e + 0 = 0

• misalkan 1 ∈  Z4
  1 + e = e + 1 = 1

• misalkan 2 ∈  Z4
  2 + e = e + 2 = 2

• misalkan 3 ∈  Z4
  3 + e = e + 3 = 3

maka Z4 ada unsur satuan atau identitas
-          Adanya unsur balikan atau invers

• Ambil sebarang nilai dari Z4, misalkan 0 ∈  Z4, pilih 0 ∈  Z4,
  sehingga 0 + 0 = 0 = e, maka (0)^-1 = 0

• Ambil sebarang nilai dari Z4, misalkan 1 ∈  Z4, pilih 3 ∈  Z4,
  sehingga 1 + 3 = 0 = e, maka (1)^-1 = 3

• Ambil sebarang nilai dari Z4, misalkan 2 ∈  Z4, pilih 2 ∈  Z4,
  sehingga 2 + 2 = 0 = e, maka (2)^-1 = 2

• Ambil sebarang nilai dari Z4, misalkan 3 ∈  Z4, pilih 1 ∈  Z4,
  sehingga 3 + 1 = 0 = e, maka (3)^-1 = 1

maka Z4 ada unsur balikan atau invers
-          Komutatif
Ambil sebarang nilai dari Z4, misalkan a = 2, b = 3 ∈  Z4
(a + b) = (2 + 3) = 1
(b + a) = (3 + 2) = 1
Sehingga :
(a + b) = (b + a) = 1
maka Z4 komutatif
Jadi, Z4 = {0, 1, 2, 3} merupakan Grup Komutatif terhadap penjumlahan (Z4, +).
2. Semigrup terhadap perkalian (Z4,.)
-          Tertutup
Ambil sebarang nilai dari Z4, misalkan 0, 1, 2, 3 ∈  Z4
1 . 0 = 0
1 . 1 = 1
1 . 2 = 2
1 . 3 = 3
karena hasilnya 0, 1, 2, 3 ∈  Z4, maka tertutup terhadap Z4
-          Assosiatif
Ambil sebarang nilai dari Z4, misalkan a = 2, b = 1 dan c = 3 ∈  Z4
(a . b) . c = (2 . 1) . 3 = 2 . 3 = 2
a . (b . c) = 2 . (1 . 3) = 2 . 3 = 2
Sehingga :
(a . b) . c = a . (b . c) = 2
maka Z4 assosiatif
Jadi, Z4 = {0, 1, 2, 3} merupakan Semigrup terhadap perkalian (Z4, .).
3. Distributif perkalian terhadap penjumlahan
Ambil sebarang nilai dari Z4, misalkan a = 2, b = 1 dan c = 3 ∈  Z4
a.(b + c) = 2.(1 + 3)
= 2.(0)
= 0
(a.b) + (a.c) = (2.1) + (2.3)
= 2 + 6
= 0
Maka, a.(b + c) = (a.b) + (a.c) = 0
(a + b).c = (2 + 1).3
= (3).3
= 1
(a.c) + (b.c) = (2.3) + (1.3)
= 2 + 3
= 1
Maka, (a + b).c = (a.c) + (b.c) = 1
Jadi, Z4 = {0, 1, 2, 3} distributif perkalian terhadap penjumlahan.
Karena Z4 = {0, 1, 2, 3} memenuhi semua aksioma-aksioma yang ada, maka Z4 adalah suatu Ring (Z4,+,.).