Look Around: HIPERBOLA

Rabu, 12 Desember 2012

HIPERBOLA

Bagi pembaca yang ingin belajar hiperbola, terlebih dahulu harus mengetahui tentang ellips. Karena hiperbola dan ellips ini sangat erat hubungannya, khususnya pada bentuk persamaannya. Parabola, hiperbola dan ellips, adalah hasil dari suatu pengirisan dari kerucut.

Suatu kerucut jika diiris horizontal, maka irisannya berbentuk lingkaran. Jika kerucut tersebut dipotong secara miring (dan tidak memotong alasnya), maka terbentuk suatu ellips. Jika mengirisnya memotong alasnya dan memotongnya secara vertikal, maka terbentuk suatu hiperbola. Jika mengirisnya memotong alasnya dan memotongnya tidak secara vertikal, maka terbentuk suatu parabola.

Kita mengetahui persamaan ellips itu adalah

$\frac{x^2}{a^2}+ \frac{y^2}{b^2}=1$

Persamaan hiperbola hampir sama dengan persamaan ellips. Hanya saja tandanya bukan positif, tetapi negatif. Persamaan hiperbola adalah sebagai berikut :

$\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$

Bagaimana gambar grafik dari suatu hiperbola?

Contohnya saja gambar grafik dari persamaan : 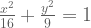$\frac{x^2}{16}+ \frac{y^2}{9}=1$

Apakah punya bayangan untuk menghubungkan persamaannya dengan gambar grafiknya?

Ketika y=0, maka 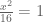$\frac{x^2}{16}=1$ sehingga $x= \pm 4$

Kita ke perumumannya saja di sini.

$\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$

Ketika y=0, maka $x= \pm a$ , a inilah yang kita sebut sebagai puncak

Apa peran b?

Ketika kita menuliskan persamaan hiperbola dalam x, maka kita bisa menulsikan

$\frac{x^2}{a^2}- 1= \frac{y^2}{b^2}$

$\frac{(x^2-a^2)(b^2)}{a^2}=y^2$

$\pm \sqrt{\frac{(x^2-a^2)(b^2)}{a^2}}=y$

$y= \pm \frac{b}{a} \sqrt{x^2-a^2}$

Untuk nilai x yang besar, 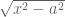$\sqrt{x^2-a^2}$ bersifat seperti x, yaitu jika 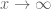$x \to \infty$ maka $\sqrt{x^2-a^2}-x \to 0$ . Sehingga y bersifat seperti

$y= \frac{b}{a}x$ atau $y=- \frac{b}{a}x$

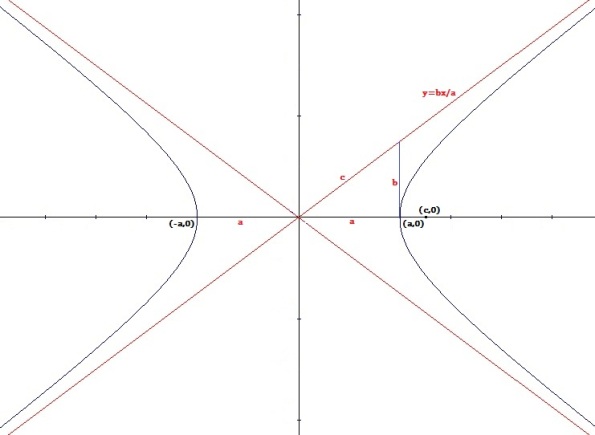
Dua garis tersebut adalah asimtot dari grafik persamaan hiperbola.

Kita sudah mendapat b (perhatikan gambar), perhatikan segitiga dengan sisi a, b dan c pada gambar. Kita mendapatkan $c^2=a^2+b^2$ , koordinat titik fokusnya yaitu (c,0)

UNTUK PARABOLA VERTIKAL, PEMBACA BISA MENYESUAIKAN

(ada 1 soal hiperbola vertikal, yaitu nomor 3)

SOAL :

1. Tentukan kedua titik fokus dari hiperbola : 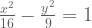$\frac{x^2}{16}- \frac{y^2}{9}=1$

Jawab :

$\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$ jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. Tentu c kita cari dengan rumus $c^2=a^2+b^2$ , dan kita dapatkan c=5.

Sehingga koordinat titik fokus dari hiperbola tersebut adalah $( pm 5,0)$

2. Tentukan garis asimtot dari hiperbola : 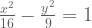$\frac{x^2}{16}- \frac{y^2}{9}=1$

Jawab :

$\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$ jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. Kedua asimtotnya kita kenal sebagai $y= \pm \frac{b}{a}x$ , maka kita peroleh kedua asimtotnya adalah $y= \pm \frac{3}{4}x$

3. Soal untuk hiperbola vertikal.

Tentukan kedua titik puncak, titik fokus dan garis asimtot untuk hiperbola : $\frac{y^2}{16}- \frac{x^2}{9}=1$ atau bisa juga dituliskan : $- \frac{x^2}{9}+ \frac{y^2}{16}=1$

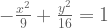
Jawab :

Ketika kita mengambil y=0, kita tidak mungkin bisa menemukan nilai x. karena bentuk 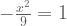$- \frac{x^2}{9}=1$ adalah tidak akan terpenuhi untuk x berapapun.

Kita ambil x=0, maka kita dapatkan y=4. Inilah puncaknya. (gambar saja coret-coretan di x=4 dan x=-4 sebagai puncak, kemudian gambar hiperbola sederhana)

Perhatikan persamaan umum yang kita gunakan : $\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$

(a itu miliknya x, berada di bawah (sebagai penyebut) dari x dan b itu miliknya y, berada di bawah (sebagai penyebut) dari y)

Sehingga, untuk soal : 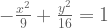$- \frac{x^2}{9}+ \frac{y^2}{16}=1$

Kita dapatkan a=3 dan b=4

Sehingga garis asimtotnya pun adalah $y= \pm \frac{4}{3}x$

Untuk mencari titik fokus, kita perlu mencari c, yaitu kita dapatkan c itu sama dengan 5. Karena hiperbola vertikal, maka koordinat titik c adalah 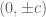$(0, \pm c)$ yaitu sama dengan $(0, \pm 5)$